12 Optimality properties and conclusion

12.1 Properties of maximum likelihood encountered so far

MLE is a special case of KL divergence minimisation valid for large samples.
MLE can be seen as generalisation of least squares (and conversely, least squares is a special case of ML).

\[\begin{align*} \begin{array}{cc} \text{Kullback-Leibler 1951}\\ \textbf{Entropy learning: minimise } D_{\text{KL}}(F_{\text{true}},F_{\boldsymbol \theta})\\ \downarrow\\ \text{large } n\\ \downarrow\\ \text{Fisher 1922}\\ \textbf{Maximise Likelihood } L(\boldsymbol \theta|D)\\ \downarrow\\ \text{normal model}\\ \downarrow\\ \text{Gauss 1805}\\ \textbf{Minimise squared error } \sum_i (x_i-\theta)^2\\ \end{array} \end{align*}\]

Given a model, derivation of the MLE is basically automatic (only optimisation required)!
MLEs are consistent, i.e. if the true underlying model \(F_{\text{true}}\) with parameter \(\boldsymbol \theta_{\text{true}}\) is contained in the set of specified candidates models \(F_{\boldsymbol \theta}\) then the MLE will converge to the true model.
Correspondingly, MLEs are asympotically unbiased.
However, MLEs are not necessarily unbiased in finite samples (e.g. the MLE of the variance parameter in the normal distribution).
The maximum likelihood is invariant against parameter transformations.
In regular situations (when local quadratic approximation is possible) MLEs are asympotically normally distributed, with the asymptotic variance determined by the observed Fisher information.
In regular situations and for large sample size MLEs are asympotically optimally efficient (Cramer-Rao theorem): For large samples the MLE achieves the lowest possible variance possible in an estimator — this is the so-called Cramer-Rao lower bound. The variance decreases to zero with \(n \rightarrow \infty\) typically with rate \(1/n\).
The likelihood ratio can be used to construct optimal tests (in the sense of the Neyman-Pearson theorem).

12.2 Summarising data and the concept of (minimal) sufficiency

Induced partioning of data space and likelihood equivalence

Every sufficient statistic \(t(D)\) induces a partitioning of the space of data sets by clustering all hypothetical outcomes for which the statistic \(t(D)\) assumes the same value \(t\): \[\mathcal{X}_t = \{D: t(D) = t\}\] The data sets in \(\mathcal{X}_t\) are equivalent in terms of the sufficient statistic \(t(D)\). Note that this implies that \(t(D)\) is not a 1:1 transformation of \(D\). Instead of \(n\) data points \(x_1, \ldots, x_n\) as few as one or two summaries (such as empirical mean and variance) may be sufficient to fully convey all the information in the data about the model parameters. Thus, transforming data \(D\) using a sufficient statistic \(t(D)\) may result in substantial data reduction.

Two data sets \(D_1\) and \(D_2\) for which the ratio of the corresponding likelihoods \(L(\boldsymbol \theta| D_1 )/L(\boldsymbol \theta| D_2)\) does not depend on \(\boldsymbol \theta\) (so the two likelihoods are proportional to each other by a constant) are called likelihood equivalent because a likelihood-based procedure to learn about \(\boldsymbol \theta\) will draw identical conclusions from \(D_1\) and \(D_2\). For data sets \(D_1, D_2 \in \mathcal{X}_t\) which are equivalent with respect to a sufficient statistic \(T\) it follows directly from the Fisher-Pearson factorisation that the ratio \[L(\boldsymbol \theta| D_1 )/L(\boldsymbol \theta| D_2) = k(D_1)/ k(D_2)\] and thus is constant with regard to \(\boldsymbol \theta\). As a result, all data sets in \(\mathcal{X}_t\) are likelihood equivalent. However, the converse is not true: depending on the sufficient statistics there usually will be many likelihood equivalent data sets that are not part of the same set \(\mathcal{X}_t\).

Minimal sufficient statistics

Of particular interest is therefore to find those sufficient statistics that achieve the coarsest partitioning of the sample space and thus may allow the highest data reduction. Specifically, a minimal sufficient statistic is a sufficient statistic for which all likelihood equivalent data sets also are equivalent under this statistic.

Therefore, to check whether a sufficient statistic \(t(D)\) is minimally sufficient we need to verify whether for any two likelihood equivalent data sets \(D_1\) and \(D_2\) it also follows that \(t(D_1) = t(D_2)\). If this holds true then \(T\) is a minimally sufficient statistic.

An equivalent non-operational definition is that a minimal sufficient statistic \(t(D)\) is a sufficient statistic that can be computed from any other sufficient statistic \(S(D)\). This follows from the above directly: assume any sufficient statistic \(S(D)\), this defines a corresponding set \(\mathcal{X}_s\) of likelihood equivalent data sets. By implication any \(D_1, D_2 \in \mathcal{X}_s\) will necessarily also be in \(\mathcal{X}_t\), thus whenever \(S(D_1)=S(D_2)\) we also have \(t(D_1)=t(D_2)\), and therefore \(t(D_1)\) is a function of \(S(D_1)\).

A trivial but important example of a minimal sufficient statistic is the likelihood function itself since by definition it can be computed from any set of sufficient statistics. Thus the likelihood function \(L(\boldsymbol \theta)\) captures all information about \(\boldsymbol \theta\) that is available in the data. In other words, it provides an optimal summary of the observed data with regard to a model. Note that in Bayesian statistics (to be discussed in Part 2 of the module) the likelihood function is used as proxy/summary of the data.

Example: normal distribution

Example 12.1 Sufficient statistics for the parameters of the normal distribution:

The normal model \(N(\mu, \sigma^2)\) with parameter vector \(\boldsymbol \theta= (\mu, \sigma^2)^T\) and log-likelihood \[ l_n(\boldsymbol \theta) = -\frac{n}{2} \log(2 \pi \sigma^2) - \frac{1}{2 \sigma^2} \sum_{i=1}^n (x_i-\mu)^2 \] One possible set of minimal sufficient statistics for \(\boldsymbol \theta\) are \(\bar{x}\) and \(\overline{x^2}\), and with these we can rewrite the log-likelihood function without any reference to the original data \(x_1, \ldots, x_n\) as follows \[ l_n(\boldsymbol \theta) = -\frac{n}{2} \log(2 \pi \sigma^2) -\frac{n}{2 \sigma^2} (\overline{x^2} - 2 \bar{x} \mu + \mu^2) \] An alternative set of minimal sufficient statistics for \(\boldsymbol \theta\) consists of \(s^2 = \overline{x^2} - \bar{x}^2 = \widehat{\sigma^2}_{ML}\) as and \(\bar{x} = \hat{\mu}_{ML}\). The log-likelihood written in terms of \(s^2\) and \(\bar{x}\) is \[ l_n(\boldsymbol \theta) = -\frac{n}{2} \log(2 \pi \sigma^2) -\frac{n}{2 \sigma^2} (s^2 + (\bar{x} - \mu)^2 ) \]

Note that in this example the dimension of the parameter vector \(\boldsymbol \theta\) equals the dimension of the minimal sufficient statistic, and furthermore, that the MLEs of the parameters are in fact minimal sufficient!

MLEs of parameters of an exponential family are minimal sufficient statistics

The conclusion from Example 12.1 holds true more generally: in an exponential family model (such as the normal distribution as particular important case) the MLEs of the parameters are minimal sufficient statistics. Thus, there will typically be substantial dimension reduction from the raw data to the sufficient statistics.

However, outside exponential families the MLE is not necessarily a minimal sufficient statistic, and may not even be a sufficient statistic. This is because a (minimal) sufficient statistic of the same dimension as the parameters does not always exist. A classic example is the Cauchy distribution for which the minimal sufficient statistics are the ordered observations, thus the MLE of the parameters do not constitute sufficient statistics, let alone minimal sufficient statistics. However, the MLE is of course still a function of the minimal sufficient statistic.

In summary, the likelihood function acts as perfect data summariser (i.e. as minimally sufficient statistic), and in exponential families (e.g. normal distribution) the MLEs of the parameters \(\hat{\boldsymbol \theta}_{ML}\) are minimal sufficient.

Finally, while sufficiency is clearly a useful concept for data reduction one needs to keep in mind that this is always in reference to a specific model. Therefore, unless one strongly believes in a certain model it is generally a good idea to keep (and not discard!) the original data.

12.3 Concluding remarks on maximum likelihood

Application of KL divergence in statistics

In statistics the typical roles of the distribution \(Q\) and \(P\) in the KL divergence \(D_{\text{KL}}(Q, P)\) are:

\(Q\) is the (unknown) underlying true model for the data generating process
\(P\) is the approximating model (typically a parametric distribution family)

Optimising (i.e. minimising) the KL divergence with regard to \(P\) amounts to approximation and optimising with regard to \(Q\) to imputation.

In previous chapters we have seen how the KL divergence leads to the maximum likelihood (via minimum cross-entropy) and also allows to choose distribution families (via maximum entropy) Later we will also see how KL divergence is linked to Bayesian learning, respectively.

Since the KL divergence is not symmetric there two distinct ways to minimise the divergence between a fixed \(F_0\) and the family \(F_{\boldsymbol \theta}\) (see Figure 12.1). minimising the parameter \(\boldsymbol \theta\) in \(D_{\text{KL}}(\hat{F}_0,F_{\boldsymbol \theta})\) (“forward KL”) and in \(D_{\text{KL}}(F_{\boldsymbol \theta}, \hat{F}_0)\) (“backward KL”).

Each way has different properties:

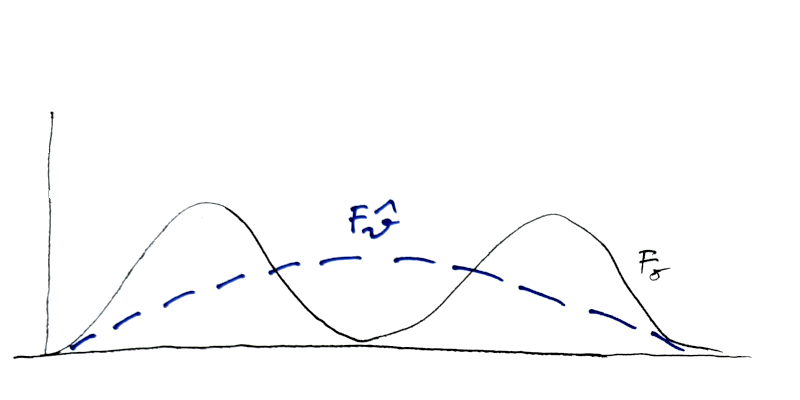
forward KL, approximation KL: \(\min_{\boldsymbol \theta} D_{\text{KL}}(F_0,F_{\boldsymbol \theta})\)

Here we keep the first argument fixed and minimise KL by changing the second argument. This is also called an “M (Moment) projection”. It has a zero avoiding property: \(f_{\boldsymbol \theta}(x)>0 \text{ whenever } f_0(x)>0\).

This procedure is mean-seeking and inclusive, i.e. when there are multiple modes in the density of \(F_0\) a fitted unimodal density \(F_{\hat{\boldsymbol \theta}}\) will seek to cover all modes (mass covering property).

Maximum likelihood is based on “forward KL”.
reverse KL, inference KL: \(\min_{\boldsymbol \theta} D_{\text{KL}}(F_{\boldsymbol \theta},F_0)\)

Here we keep the second argument fixed and minimise KL by changing the first argument. This is also called an “I (Information) projection”. It has a zero forcing property: \(f_{\boldsymbol \theta}(x)=0 \text{ whenever } f_0(x)=0\).

This procedure is mode-seeking and exclusive, i.e. when there are multiple modes in the density of \(F_0\) a fitted unimodal density \(F_{\hat{\boldsymbol \theta}}\) will seek out one mode to the exclusion of the others (mode attracting property).

Bayesian updating and variational Bayes approximations use “reverse KL”.

What happens if \(n\) is small?

From the long list of optimality properties of ML it is clear that for large sample size \(n\) the best estimator will typically be the MLE.

However, for small sample size it is indeed possible (and necessary) to improve over the MLE (e.g. via Bayesian estimation or regularisation). Some of these ideas will be discussed in Part II.

Likelihood will overfit!

Alternative methods need to be used:

regularised/penalised likelihood
Bayesian methods

which are essentially two sides of the same coin.

Classic example of a simple non-ML estimator that is better than the MLE: Stein’s example / Stein paradox (C. Stein, 1955):

Problem setting: estimation of the mean in multivariate case
Maximum likelihood estimation breaks down! \(\rightarrow\) average (=MLE) is worse in terms of MSE than Stein estimator.
For small \(n\) the asymptotic distributions for the MLE and for the LRT are not accurate, so for inference in these situations the distributions may need to be obtained by simulation (e.g. parametric or nonparametric bootstrap).

Model selection

CI are sets of models that are not statistically distinguishable from the best ML model
in doubt, choose the simplest model compatible with data
better prediction, avoids overfitting
Useful for model exploration and model building.
Note that, by construction, the model with more parameters always has a higher likelihood, implying likelihood favours complex models
Complex model may overfit!
For comparison of models penalised likelihood or Bayesian approaches may be necessary
Model selection in small samples and high dimension is challenging
Recall that the aim in statistics is not about rejecting models (this is easy as for large sample size any model will be rejected!)
Instead, the aim is model building, i.e. to find a model that explains the data well and that predicts well!
Typically, this will not be the best-fit ML model, but rather a simpler model that is close enough to the best / most complex model.