5 Multivariate distributions
5.1 Multinomial distribution
The multinomial distribution \(\text{Mult}(n, \boldsymbol \theta)\) is the multivariate generalisation of the binomial distribution \(\text{Bin}(n, \theta)\) (Section 4.1) from two classes to \(K\) classes.
A special case is the categorical distribution \(\text{Cat}(\boldsymbol \theta)\) that generalises the Bernoulli distribution \(\text{Ber}(\theta)\).
Standard parametrisation
A multinomial random variable \(\boldsymbol x\) describes describes the allocation of \(n\) items to \(K\) classes. We write \[ \boldsymbol x\sim \text{Mult}(n, \boldsymbol \theta) \] where the parameter vector \(\boldsymbol \theta=(\theta_1, \ldots, \theta_K)^T\) specifies the probability of each of \(K\) classes, with \(\theta_i \in [0,1]\) and \(\boldsymbol \theta^T \mathbf 1_K = \sum_{i=1}^K \theta_i = 1\). Thus there are \(K-1\) independent elements in \(\boldsymbol \theta\). The number of classes \(K\) is implicitly given by the dimension of the vector \(\boldsymbol \theta\). Each element of the vector \(\boldsymbol x= (x_1, \ldots, x_K)^T\) is an integer \(x_i \in \{0, 1, \ldots, n\}\) and \(\boldsymbol x\) satisfies the constraint \(\boldsymbol x^T \mathbf 1_K = \sum_{i=1}^K x_i = n\). Therefore the support of \(\boldsymbol x\) is a \(K-1\) dimensional space and it notably depends on \(n\).
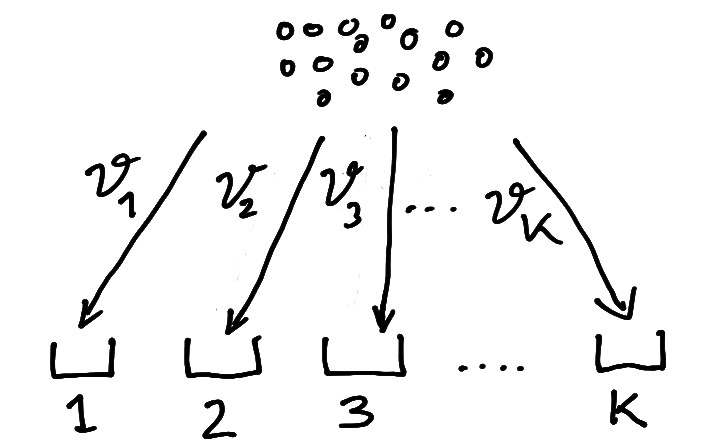
The multinomial distribution is best illustrated by an urn model distributing \(n\) items into \(K\) bins where \(\boldsymbol \theta\) contains the corresponding bin probabilities (Figure 5.1).
The expected value is \[ \text{E}(\boldsymbol x) = n \boldsymbol \theta \] The covariance matrix is \[ \text{Var}(\boldsymbol x) = n (\text{Diag}(\boldsymbol \theta) - \boldsymbol \theta\boldsymbol \theta^T) \] The covariance matrix is singular by construction because of the dependencies among the elements of \(\boldsymbol x\).
The corresponding pmf is \[ p(\boldsymbol x| \boldsymbol \theta) = \binom{n}{x_1, \ldots, x_n} \prod_{i=1}^K \theta_i^{x_i} \] where \(\binom{n}{x_1, \ldots, x_n}\) is the multinomial coefficient. While all \(K\) elements of \(\boldsymbol x\) appear in the pmf recall that due the dependencies among the \(x_i\) the pmf is defined over a \(K-1\) dimensional support.
For \(K=2\) the multinomial distribution reduces to the binomial distribution (Section 4.1).
The pmf of the multinomial distribution is given by dmultinom(). The corresponding random number generator is rmultinom().
Mean parametrisation
Instead of \(\boldsymbol \theta\) one may also use a mean parameter \(\boldsymbol \mu\), with elements \(\mu_i \in [0,n]\) and \(\boldsymbol \mu^T \mathbf 1_K = \sum^{K}_{i=1}\mu_i = n\), so that \[ \boldsymbol x\sim \text{Mult}\left(n, \boldsymbol \theta= \frac{\boldsymbol \mu}{n}\right) \] The mean parameter \(\boldsymbol \mu\) can be obtained from \(\boldsymbol \theta\) and \(n\) by \(\boldsymbol \mu= n \boldsymbol \theta\). Note that the parameter space for \(\boldsymbol \mu\) and the support of \(\boldsymbol x\) are both of dimension \(K-1\).
The mean and variance of the multinomial distribution expressed in terms of \(\boldsymbol \mu\) and \(n\) are \[ \text{E}(x) = \boldsymbol \mu \] and \[ \text{Var}(x) = \text{Diag}(\boldsymbol \mu) - \frac{\boldsymbol \mu\boldsymbol \mu^T}{n} \] The covariance matrix is singular by construction because of the dependencies among the elements of \(\boldsymbol x\).
Special case: categorical distribution
For \(n=1\) the multinomial distribution reduces to the categorical distribution \(\text{Cat}(\boldsymbol \theta)\) which in turn is the multivariate generalisation of the Bernoulli distribution \(\text{Ber}(\theta)\) from two classes to \(K\) classes.
If a random variable \(\boldsymbol x\) follows the categorical distribution we write \[ \boldsymbol x\sim \text{Cat}(\boldsymbol \theta) \] with class probabilities \(\boldsymbol \theta\) and \(\boldsymbol \theta^T \mathbf 1_K = 1\). The support is \(x_i \in \{0, 1\}\) and \(\boldsymbol x^T \mathbf 1_K =1\) and is a \(K-1\) dimensional space.
The random vector \(\boldsymbol x\) takes the form of an indicator vector \(\boldsymbol x= (x_1, \ldots, x_K)^T = (0, 0, \ldots, 1, \ldots, 0)^T\) containing zeros everywhere except for a single element \(x_k=1\) indicating the class \(k\) to which the item has been allocated. This is called “one hot encoding”, as opposed to “integer encoding”, i.e. stating the class number \(k\).
The expected value is \[ \text{E}(\boldsymbol x) = \boldsymbol \theta \] The covariance matrix is \[ \text{Var}(\boldsymbol x) = \text{Diag}(\boldsymbol \theta) - \boldsymbol \theta\boldsymbol \theta^T \] The covariance matrix is singular by construction because of the dependencies among the elements of \(\boldsymbol x\). This follows directly from the definition of the variance \(\text{Var}(\boldsymbol x) = \text{E}( \boldsymbol x\boldsymbol x^T) - \text{E}( \boldsymbol x) \text{E}( \boldsymbol x)^T\) and noting that \(x_i^2 = x_i\) and \(x_i x_j = 0\) if \(i \neq j\).
The corresponding pmf is \[ p(\boldsymbol x| \boldsymbol \theta) = \prod_{k=1}^K \theta_k^{x_k} = \begin{cases} \theta_k & \text{if } x_k = 1 \\ \end{cases} \] Recall that the pmf is defined over the \(K-1\) dimensional support of \(\boldsymbol x\).
For \(K=2\) the categorical distribution reduces to the Bernoulli \(\text{Ber}(\theta)\) distribution, with \(\theta_1=\theta\), \(\theta_2=1-\theta\) and \(x_1=x\) and \(x_2=1-x\).
Convolution property
The convolution of \(n\) multinomial distributions, each with identical bin probabilities \(\boldsymbol \theta\) but possibly different number of items \(n_i\), yields another multinomial distribution with the same parameter \(\boldsymbol \theta\): \[ \sum_{i=1}^n \text{Mult}(n_i, \boldsymbol \theta) \sim \text{Mult}\left(\sum_{i=1}^n n_i, \boldsymbol \theta\right) \]
It follows that the multinomial distribution with \(n\) items is the result of the convolution of \(n\) categorical distributions: \[ \sum_{i=1}^n \text{Cat}(\boldsymbol \theta) \sim \text{Mult}(n, \boldsymbol \theta) \] Thus, repeating the same categorical trial \(n\) times and counting the total number of allocations in each bin yields a multinomial random variable.
5.2 Dirichlet distribution
The Dirichlet distribution \(\text{Dir}(\boldsymbol \alpha)\) is the multivariate generalisation of the beta distribution \(\text{Beta}(\alpha_1, \alpha_2)\) (Section 4.2) that is useful to model proportions or probabilities for \(K\geq 2\) classes. It is named after Peter Gustav Lejeune Dirichlet (1805–1859).
It includes the uniform distribution over the \(K-1\) unit simplex as special case.
Standard parametrisation
A Dirichlet distributed random vector is denoted by \[ \boldsymbol x\sim \text{Dir}(\boldsymbol \alpha) \] with shape parameter \(\boldsymbol \alpha= (\alpha_1,...,\alpha_K)^T >0\) and \(K\geq 2\). Let \(m = \boldsymbol \alpha^T \mathbf 1_K = \sum^{K}_{i=1}\alpha_i\). The support of \(\boldsymbol x\) is the \(K-1\) dimensional unit simplex given by \(x_i \in [0,1]\) and \(\boldsymbol x^T \mathbf 1_K = \sum^{K}_{i=1} x_i = 1\). Thus, the Dirichlet distribution is defined over a \(K-1\) dimensional space.
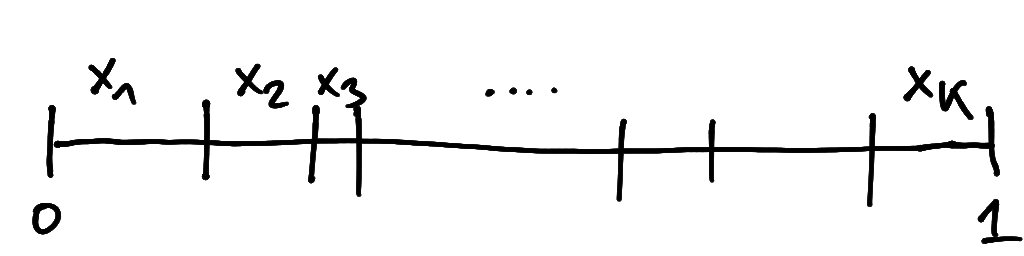
A Dirichlet random variable can be visualised as breaking a unit stick into \(K\) individual pieces of lengths \(x_1, x_2, \ldots, x_K\) adding up to one (Figure 5.2). Thus, the \(x_i\) may be used as the exclusive proportions or probabilities for \(K\) classes.
The mean is \[ \text{E}(\boldsymbol x) = \frac{\boldsymbol \alpha}{m } \] and the variance is \[ \text{Var}\left(\boldsymbol x\right) = \frac{ m \text{Diag}(\boldsymbol \alpha)-\boldsymbol \alpha\boldsymbol \alpha^T}{m^2(m+1)} \] The covariance matrix is singular by construction because of the dependencies among the elements of \(\boldsymbol x\). In component notation it is \[ \text{Cov}(x_i,x_j) = \frac{[i=j] m \alpha_i - \alpha_i \alpha_j}{m^2(m+1)} \] where the indicator function \([i=j]\) equals 1 if \(i=j\) and 0 otherwise.
The pdf of the Dirichlet distribution \(\text{Dir}(\boldsymbol \alpha)\) is \[ p(\boldsymbol x| \boldsymbol \alpha) = \frac{1}{B(\boldsymbol \alpha)} \prod_{k=1}^K x_k^{\alpha_k-1} \] This depends on the beta function with multivariate argument \(\boldsymbol \alpha\) defined as \[ B(\boldsymbol \alpha) = \frac{ \prod_{k=1}^K \Gamma(\alpha_k) }{\Gamma(m )} \] While all \(K\) elements of \(\boldsymbol x\) appear in the pdf recall that due the dependencies among the \(x_i\) the pdf is defined over a \(K-1\) dimensional support.
For \(K=2\) the Dirichlet distribution reduces to the beta distribution (Section 4.2).
The extraDistr package implements the Dirichlet distribution. The pmf of the Dirichlet distribution is given by extraDistr::ddirichlet(). The corresponding random number generator is extraDistr::rdirichlet().
Mean parametrisation
Instead of employing \(\boldsymbol \alpha\) as parameter vector another useful reparametrisation of the Dirichlet distribution is in terms of a mean parameter \(\boldsymbol \mu\), with elements \(\mu_i \in [0,1]\) and \(\boldsymbol \mu^T \mathbf 1_K = \sum^{K}_{i=1}\mu_i = 1\), and a concentration parameter \(m > 0\) so that \[ \boldsymbol x\sim \text{Dir}(\boldsymbol \alpha=m \boldsymbol \mu) \] The concentration and mean parameters can be obtained from \(\boldsymbol \alpha\) by \(m = \boldsymbol \alpha^T \mathbf 1_K\) and \(\boldsymbol \mu= \boldsymbol \alpha/m\). The space of possible values for the mean parameter \(\boldsymbol \mu\) and the support of \(\boldsymbol x\) are both of dimension \(K-1\).
The mean and variance of the Dirichlet distribution expressed in terms of \(\boldsymbol \mu\) and \(m\) are \[ \text{E}(\boldsymbol x) = \boldsymbol \mu \] and \[\text{Var}\left(\boldsymbol x\right) = \frac{ \text{Diag}(\boldsymbol \mu)-\boldsymbol \mu\boldsymbol \mu^T}{m+1}\] The covariance matrix is singular by construction because of the dependencies among the elements of \(\boldsymbol x\). In component notation it is \[ \begin{split} \text{Cov}(x_i,x_j) &= \frac{[i=j]\mu_i - \mu_i \mu_j}{m+1} \\ &= \begin{cases} \mu_i(1-\mu_i)/(m+1) & \text{if $i=j$}\\ -\mu_i \mu_j / (m+1) & \text{if $i\neq j$}\\ \end{cases}\\ \end{split} \]
Special case: symmetric Dirichlet distribution
For \(\boldsymbol \alpha= \alpha \mathbf 1_K\) the Dirichlet distribution becomes the symmetric beta distribution with a single shape parameters \(\alpha>0\). In mean parametrisation the symmetric Dirichlet distribution corresponds to \(\boldsymbol \mu=\mathbf 1_K/K\) and \(m=\alpha K\).
Special case: uniform distribution
For \(\boldsymbol \alpha= \mathbf 1_K\) the Dirichlet distribution becomes the uniform distribution over the \(K-1\) unit simplex with pdf \(p(\boldsymbol x)=1/\Gamma(K)\). In mean parametrisation the symmetric Dirichlet distribution corresponds to \(\boldsymbol \mu=\mathbf 1_K/K\) and \(m=K\).
5.3 Multivariate normal distribution
The multivariate normal distribution \(N(\boldsymbol \mu, \boldsymbol \Sigma)\) generalises the univariate normal distribution \(N(\mu, \sigma^2)\) (Section 4.3) from one to \(d\) dimensions.
A special case is the multivariate standard normal distribution \(N(\mathbf 0, \boldsymbol I)\).
Standard parametrisation
The multivariate normal distribution \(N(\boldsymbol \mu, \boldsymbol \Sigma)\) has a mean or location parameter \(\boldsymbol \mu\) (a \(d\) dimensional vector), a variance parameter \(\boldsymbol \Sigma\) (a \(d \times d\) positive definite symmetric matrix) and support \(\boldsymbol x\in \mathbb{R}^d\).
If a random vector \(\boldsymbol x= (x_1, x_2,...,x_d)^T\) follows a multivariate normal distribution we write \[ \boldsymbol x\sim N(\boldsymbol \mu, \boldsymbol \Sigma) \] with mean \[ \text{E}(\boldsymbol x) = \boldsymbol \mu \] and variance \[ \text{Var}(\boldsymbol x) = \boldsymbol \Sigma \] In the above notation the dimension \(d\) is implicitly given by the dimensions of \(\boldsymbol \mu\) and \(\boldsymbol \Sigma\) but for clarity one often also writes \(N_d(\boldsymbol \mu, \boldsymbol \Sigma)\) to explicitly indicate the dimension.
The pdf is given by \[ \begin{split} p(\boldsymbol x| \boldsymbol \mu, \boldsymbol \Sigma) &= \det(2 \pi \boldsymbol \Sigma)^{-1/2} \exp\left(-\frac{1}{2} (\boldsymbol x-\boldsymbol \mu)^T \boldsymbol \Sigma^{-1} (\boldsymbol x-\boldsymbol \mu) \right)\\ &= \det(\boldsymbol \Sigma)^{-1/2} (2\pi)^{-d/2} e^{-\Delta^2 /2}\\ \end{split} \] Here \(\Delta^2 = (\boldsymbol x-\boldsymbol \mu)^T \boldsymbol \Sigma^{-1} (\boldsymbol x-\boldsymbol \mu)\) is the squared Mahalanobis distance between \(\boldsymbol x\) and \(\boldsymbol \mu\) taking into account the variance \(\boldsymbol \Sigma\). Note that this pdf is a joint pdf over the \(d\) elements \(x_1, \ldots, x_d\) of the random vector \(\boldsymbol x\).
The multivariate normal distribution is sometimes also used by specifying the precision matrix \(\boldsymbol \Sigma^{-1}\) instead of the variance \(\boldsymbol \Sigma\).
For \(d=1\) the random vector \(\boldsymbol x=x\) is a scalar, \(\boldsymbol \mu= \mu\), \(\boldsymbol \Sigma= \sigma^2\) and thus the multivariate normal distribution reduces to the univariate normal distribution (Section 4.3).
The mnormt package implements the multivariate normal distribution. The function mnormt::dmnorm() provides the pdf and mnormt::pmnorm() returns the distribution function. The function mnormt::rmnorm() is the corresponding random number generator.
The mniw package also implements the multivariate normal distribution. The pdf of the Wishart distribution is given by mniw::dmNorm(). The corresponding random number generator is mniw::rmNorm().
Scale parametrisation
In the univariate case it is straightforward to use the standard deviation \(\sigma\) as scale parameter instead of the variance \(\sigma^2\), and similarly the inverse standard deviation \(w=1/\sigma\) instead of the precision \(\sigma^{-2}\). However, in the multivariate setting with a matrix variance parameter \(\boldsymbol \Sigma\) it is less obvious how to define a suitable matrix scale parameter.
Let \(\boldsymbol \Sigma= \boldsymbol U\boldsymbol \Lambda\boldsymbol U^T\) be the eigendecomposition of the positive definite matrix \(\boldsymbol \Sigma\). Then \(\boldsymbol \Sigma^{1/2} = \boldsymbol U\boldsymbol \Lambda^{1/2} \boldsymbol U^T\) is the principal matrix square root and \(\boldsymbol \Sigma^{-1/2} = \boldsymbol U\boldsymbol \Lambda^{-1/2} \boldsymbol U^T\) the inverse principal matrix square root. Furthermore, let \(\boldsymbol Q\) be an arbitrary orthogonal matrix with \(\boldsymbol Q^T \boldsymbol Q= \boldsymbol Q\boldsymbol Q^T = \boldsymbol I\).
Then \(\boldsymbol W= \boldsymbol Q\boldsymbol \Sigma^{-1/2}\) is called a whitening matrix based on \(\boldsymbol \Sigma\) and \(\boldsymbol L= \boldsymbol W^{-1}= \boldsymbol \Sigma^{1/2} \boldsymbol Q^T\) is the corresponding inverse whitening matrix. By construction, the matrix \(\boldsymbol L\) provides a factorisation of the covariance matrix by \(\boldsymbol L\boldsymbol L^T = \boldsymbol \Sigma\). Similarly, \(\boldsymbol W\) factorises the precision matrix by \(\boldsymbol W^T \boldsymbol W= \boldsymbol \Sigma^{-1}\). The two matrices thus provide the basis for the scale parametrisation of the multivariate normal distribution.
Specifically, the matrix \(\boldsymbol L\) is used in place of \(\boldsymbol \Sigma\) and plays the role of the matrix scale parameter (corresponding to \(\sigma\) in the univariate setting) and \(\boldsymbol W\) is used in place of the precision matrix \(\boldsymbol \Sigma^{-1}\) and plays the role of the inverse matrix scale parameter (corresponding to \(1/\sigma\) in the univariate case). The determinants occurring in the multivariate normal pdf can be rewritten in terms of \(\boldsymbol L\) and \(\boldsymbol W\) using the identities \(|\det(\boldsymbol W)|=\det(\boldsymbol \Sigma)^{-1/2}\) and \(|\det(\boldsymbol L)|=\det(\boldsymbol \Sigma)^{1/2}\) as \(\det(\boldsymbol Q) = \pm 1\).
Since \(\boldsymbol Q\) can be freely chosen the matrices \(\boldsymbol W\) and \(\boldsymbol L\) are not fully determined by \(\boldsymbol \Sigma\) alone but there is rotational freedom due to \(\boldsymbol Q\). Standard choices are
- \(\boldsymbol Q^{\text{ZCA}}=\boldsymbol I\) for ZCA-type factorisation with \(\boldsymbol W^{\text{ZCA}}=\boldsymbol \Sigma^{-1/2}\) and
- \(\boldsymbol Q^{\text{PCA}}=\boldsymbol U^T\) for PCA-type factorisation with \(\boldsymbol W^{\text{PCA}}=\boldsymbol \Lambda^{-1/2} \boldsymbol U^T\). Note that the matrix \(\boldsymbol U\) is not unique because its columns (eigenvectors) can have different signs (directions), hence \(\boldsymbol W^{\text{PCA}}\) and \(\boldsymbol L^{\text{PCA}}\) are also not unique without further constraints, such as positive diagonal elements of the (inverse) whitening matrix.
- A third common choice is to compute \(\boldsymbol L\) directly by Cholesky decomposition of \(\boldsymbol \Sigma\), which yields an \(\boldsymbol L^{\text{Chol}}\) (and also a \(\boldsymbol W^{\text{Chol}}\)) in the form of a lower-triangular matrix with a positive diagonal, and a corresponding underlying \(\boldsymbol Q^{\text{Chol}}=(\boldsymbol L^{\text{Chol}})^T \boldsymbol \Sigma^{-1/2}\).
Finally, the whitening matrix \(\boldsymbol W\) and its inverse may also be constructed from the correlation matrix \(\boldsymbol P\) and the diagonal matrix containing the variances \(\boldsymbol V\) (with \(\boldsymbol \Sigma= \boldsymbol V^{1/2} \boldsymbol P\boldsymbol V^{1/2}\)) in the form \(\boldsymbol W= \boldsymbol Q\boldsymbol P^{-1/2} \boldsymbol V^{-1/2}\) and \(\boldsymbol L= \boldsymbol V^{1/2} \boldsymbol P^{1/2} \boldsymbol Q^T\).
Special case: multivariate standard normal distribution
The multivariate standard normal distribution \(N(\mathbf 0, \boldsymbol I)\) has mean \(\boldsymbol \mu=\mathbf 0\) and variance \(\boldsymbol \Sigma=\boldsymbol I\). The corresponding pdf is \[ p(\boldsymbol x) = (2\pi)^{-d/2} e^{-\boldsymbol x^T \boldsymbol x/2 } \] with the squared Mahalanobis distance reduced to \(\Delta^2=\boldsymbol x^T \boldsymbol x= \sum_{i=1}^d x_i^2\).
The density of the multivariate standard normal distribution is the product of the corresponding univariate standard normal densities \[ p(\boldsymbol x) = \prod_{i=1}^d \, (2\pi)^{-1/2} e^{-x_i^2/2 } \] and therefore the elements \(x_i\) of \(\boldsymbol x=(x_1, \ldots, x_d)^T\) are independent of each other.
Location-scale transformation
Let \(\boldsymbol W\) be a whitening matrix for \(\boldsymbol \Sigma\) and \(\boldsymbol L\) the corresponding inverse whitening matrix.
If \(\boldsymbol x\sim N(\boldsymbol \mu, \boldsymbol \Sigma)\) then \(\boldsymbol y= \boldsymbol W(\boldsymbol x-\boldsymbol \mu) \sim N(\mathbf 0, \boldsymbol I)\). This location-scale transformation corresponds to centring and whitening (i.e. standardisation and decorrelation) of a multivariate normal random variable.
Conversely, if \(\boldsymbol y\sim N(\mathbf 0, \boldsymbol I)\) then \(\boldsymbol x= \boldsymbol \mu+ \boldsymbol L\boldsymbol y\sim N(\boldsymbol \mu, \boldsymbol \Sigma)\). This location-scale transformation generates the multivariate normal distribution from the multivariate standard normal distribution.
Note that under the location-scale transformation \(\boldsymbol x= \boldsymbol \mu+ \boldsymbol L\boldsymbol y\) with \(\text{Var}(\boldsymbol y)=\boldsymbol I\) we get \(\text{Cov}(\boldsymbol x, \boldsymbol y) = \boldsymbol L\). This provides a means to choose between different (inverse) whitening transformation and the corresponding factorisations of \(\boldsymbol \Sigma\) and \(\boldsymbol \Sigma^{-1}\). For example, if positive correlation between corresponding elements in \(\boldsymbol x\) and \(\boldsymbol y\) is desired then the diagonal elements in \(\boldsymbol L\) must be positive.
Convolution property
The convolution of \(n\) independent, but not necessarily identical, multivariate normal distributions of the same dimension \(d\) results in another \(d\)-dimensional multivariate normal distribution with corresponding mean and variance: \[ \sum_{i=1}^n N(\boldsymbol \mu_i, \boldsymbol \Sigma_i) \sim N\left( \sum_{i=1}^n \boldsymbol \mu_i, \sum_{i=1}^n \boldsymbol \Sigma_i \right) \] Hence, any multivariate normal random variable can be constructed as the sum of \(n\) suitable independent multivariate normal random variables.
Since \(n\) is an arbitrary positive integer the multivariate normal distribution is said to be infinitely divisible.
5.4 Wishart distribution
The Wishart distribution \(\text{Wis}\left(\boldsymbol S, k\right)\) is a multivariate generalisation of the gamma distribution \(\text{Gam}(\alpha, \theta)\) (Section 4.4) from one to \(d\) dimensions.
Standard parametrisation
If the symmetric random matrix \(\boldsymbol X\) of dimension \(d \times d\) is Wishart distributed we write \[ \boldsymbol X\sim \text{Wis}\left(\boldsymbol S, k\right) \] where \(\boldsymbol S=(s_{ij})\) is the scale parameter (a symmetric \(d \times d\) positive definite matrix with elements \(s_{ij}\)). The dimension \(d\) is implicit in the scale parameter \(\boldsymbol S\).
The shape parameter \(k\) takes on real values in the range \(k > d-1\) and integer values in the range \(k \in {1, \ldots, d-1}\) for \(d>1\). For \(k>d-1\) the matrix \(\boldsymbol X\) is positive definite and invertible (see also Section 5.5), otherwise \(\boldsymbol X\) is singular and positive semi-definite.
The distribution has mean \[ \text{E}(\boldsymbol X) = k \boldsymbol S \] and variances of the elements of \(\boldsymbol X\) are \[ \text{Var}(x_{ij}) = k \left(s^2_{ij}+s_{ii} s_{jj} \right) \]
The pdf is (for \(k>d-1\)) \[ p(\boldsymbol X| \boldsymbol S, k) = \frac{1}{\Gamma_d(k/2) \det(2 \boldsymbol S)^{k/2}} \det(\boldsymbol X)^{(k-d-1)/2} \exp\left(-\text{Tr}(\boldsymbol S^{-1}\boldsymbol X)/2\right) \] with the multivariate gamma function defined as \[ \Gamma_d(k/2) = \pi^{d (d-1)/4} \prod_{j=1}^d \Gamma((k - j+1)/2) \] Note that this pdf is a joint pdf over the \(d\) diagonal elements \(x_{ii}\) and the \(d(d-1)/2\) off-diagonal elements \(x_{ij}\) of the symmetric random matrix \(\boldsymbol X\).
If \(\boldsymbol S\) is a scalar rather than a matrix (and hence \(d=1\)) then the multivariate Wishart distribution reduces to the univariate Wishart aka gamma distribution (Section 4.4).
The Wishart distribution is closely related to the multivariate normal distribution with mean zero. Specifically, if \(\boldsymbol z\sim N(\mathbf 0, \boldsymbol S)\) then \(\boldsymbol z\boldsymbol z^T \sim \text{Wis}(\boldsymbol S, 1)\).
The mniw package implements the Wishart distribution. The pdf of the Wishart distribution is given by mniw::dwish(). The corresponding random number generator is mniw::rwish().
Mean parametrisation
It is useful to employ the Wishart distribution in mean parametrisation \[ \text{Wis}\left(\boldsymbol S= \frac{\boldsymbol M}{k}, k \right) \] with parameters \(\boldsymbol M= k \boldsymbol S\) and \(k\). In this parametrisation the mean is \[ \text{E}(\boldsymbol X) = \boldsymbol M= (\mu_{ij}) \] and variances of the elements of \(\boldsymbol X\) are \[ \text{Var}(x_{ij}) = \frac{ \mu^2_{ij}+\mu_{ii}\mu_{jj} }{k} \]
Special case: standard Wishart distribution
For \(\boldsymbol S=\boldsymbol I\) the Wishart distribution reduces to the standard Wishart distribution \[ \boldsymbol X\sim \text{Wis}\left(\boldsymbol I, k\right) \] with a single shape parameter \(k\). The mean is \[ \text{E}(\boldsymbol X) = k \boldsymbol I \] and variances of the elements of \(\boldsymbol X\) are \[ \text{Var}(x_{ij}) = \begin{cases} 2k & \text{if $i=j$}\\ k & \text{if $i\neq j$}\\ \end{cases} \] The pdf is (for \(k> d-1\)) \[ p(\boldsymbol X| k) = \frac{1}{\Gamma_d(k/2) 2^{d k/2}} \det(\boldsymbol X)^{(k-d-1)/2} \exp\left(-\text{Tr}(\boldsymbol X)/2\right) \]
The standard Wishart distribution is closely related to the standard multivariate normal distribution with mean zero. Specifically, if \(\boldsymbol z\sim N(\mathbf 0, \boldsymbol I)\) then \(\boldsymbol z\boldsymbol z^T \sim \text{Wis}(\boldsymbol I, 1)\).
The Bartlett decomposition of the standard multivariate Wishart \(\text{Wis}(\boldsymbol I, k)\) distribution for any real \(k > d-1\) is obtained by Cholesky factorisation of the random matrix \(\boldsymbol X= \boldsymbol Z\boldsymbol Z^T\). By construction \(\boldsymbol Z\) is a lower-triangular matrix with positive diagonal elements \(z_{ii}\) and lower off-diagonal elements \(z_{ij}\) with \(i>j\) and \(i,j \in \{1, \ldots, d\}\). The corresponding upper off-diagonal elements are set to zero (\(z_{ji}=0\)).
The \(d(d+1)/2\) elements of \(\boldsymbol Z\) are independent and allow to generate a standard Wishart variate as follows:
- the squared diagonal elements follow a univariate standard Wishart distribution \(z_{ii}^2 \sim \text{Wis}(1, k-i+1)\) and
- the off-diagonal elements follow the univariate standard normal distribution \(z_{ij}\sim N(0,1)\).
- Then \(\boldsymbol X= \boldsymbol Z\boldsymbol Z^T \sim \text{Wis}(\boldsymbol I, k)\).
Scale transformation
If \(\boldsymbol X\sim \text{Wis}(\boldsymbol S, k)\) then the scaled symmetric random matrix \(\boldsymbol A\boldsymbol X\boldsymbol A^T\) is also Wishart distributed with \(\boldsymbol A\boldsymbol X\boldsymbol A^T \sim \text{Wis}(\boldsymbol A\boldsymbol S\boldsymbol A^T, k)\) where the matrix \(\boldsymbol A\) must be full rank and \(\boldsymbol A\boldsymbol S\boldsymbol A^T\) remains positive definite. The matrix \(\boldsymbol A\) may be rectangular, hence the size of \(\boldsymbol A\boldsymbol X\boldsymbol A^T\) and \(\boldsymbol A\boldsymbol S\boldsymbol A^T\) may be smaller compared to \(\boldsymbol X\) and \(\boldsymbol S\).
The transformations between the Wishart distribution and the standard Wishart distribution are two important special cases:
With \(\boldsymbol W^T \boldsymbol W= \boldsymbol S^{-1}\) and \(\boldsymbol X\sim \text{Wis}(\boldsymbol S, k)\) then \(\boldsymbol Y= \boldsymbol W\boldsymbol X\boldsymbol W^T \sim \text{Wis}(\boldsymbol I, k)\) as \(\boldsymbol W\boldsymbol S\boldsymbol W^T=\boldsymbol I\). This transformation reduces the Wishart distribution to the standard Wishart distribution.
Conversely, with \(\boldsymbol L\boldsymbol L^T = \boldsymbol S\) and \(\boldsymbol Y\sim \text{Wis}(\boldsymbol I, k)\) then \(\boldsymbol X= \boldsymbol L\boldsymbol Y\boldsymbol L^T \sim \text{Wis}(\boldsymbol S, k)\) as \(\boldsymbol L\boldsymbol I\boldsymbol L^T=\boldsymbol S\). This transformation generates the Wishart distribution from the standard Wishart distribution.
Convolution property
The convolution of \(n\) Wishart distributions with the same scale parameter \(\boldsymbol S\) but possible different shape parameters \(k_i\) yields another Wishart distribution: \[ \sum_{i=1}^n \text{Wis}(\boldsymbol S, k_i) \sim \text{Wis}\left(\boldsymbol S, \sum_{i=1}^n k_i\right) \] Note that the shape parameter \(k\) is restricted to be an integer in the range \(1, \ldots, d-1\) for \(d>1\) but is a real number in the range \(k> d-1\). Thus, if the \(k_i\) are all valid shape parameters (for dimension \(d\)) then \(\sum_{i=1}^n k_i\) is also a valid shape parameter.
Due the partial restriction of the shape parameter \(k\) to integer values the multivariate Wishart distribution is not infinitely divisible for \(d>1\).
The above includes the following construction of the multivariate Wishart distribution \(\text{Wis}(S, k)\) for integer-valued \(k\). The sum of \(k\) independent Wishart random variables \(\text{Wis}(\boldsymbol S, 1)\) with one degree of freedom and identical scale parameter yields a Wishart random variable \(\text{Wis}(\boldsymbol S, k)\) with degree of freedom \(k\) and the same scale parameter. Thus, if \(\boldsymbol z_1,\boldsymbol z_2,\dots,\boldsymbol z_k\sim N(\mathbf 0,\boldsymbol S)\) are \(k\) independent samples from \(N(\mathbf 0,\boldsymbol S)\) then \(\sum_{i_1}^k \boldsymbol z_i \boldsymbol z_i^T \sim \text{Wis}(\boldsymbol S, k)\).
5.5 Inverse Wishart distribution
The inverse Wishart distribution \(\text{IW}\left(\boldsymbol \Psi, k\right)\) is a multivariate generalisation of the inverse gamma distribution \(\text{IG}(\alpha, \beta)\) (Section 4.5) from one to \(d\) dimensions. It is linked to the Wishart distribution \(\text{Wis}(\boldsymbol S, k)\) (Section 5.4).
Standard parametrisation
A symmetric positive definite random matrix \(\boldsymbol X\) of dimension \(d \times d\) following an inverse Wishart distribution is denoted by \[ \boldsymbol X\sim \text{IW}\left(\boldsymbol \Psi, k\right) \] where \(\boldsymbol \Psi= (\psi_{ij})\) is the scale parameter (a \(d \times d\) positive definite symmetric matrix) and \(k> d-1\) is the shape parameter. The dimension \(d\) is implicit in the scale parameter \(\boldsymbol \Psi\).
The mean is (for \(k > d+1\)) \[ \text{E}(\boldsymbol X) = \frac{\boldsymbol \Psi}{k-d-1} \] and the variances of elements of \(\boldsymbol X\) are (for \(k > d+3\)) \[ \text{Var}(x_{ij})= \frac{ (k-d-1) \, \psi_{ii} \psi_{jj} + (k-d+1)\, \psi_{ij}^2 }{ (k-d) (k-d-3) (k-d-1)^2 } \]
The inverse Wishart distribution \(\text{IW}\left(\boldsymbol \Psi, k\right)\) has pdf \[ p(\boldsymbol X| \boldsymbol \Psi, k) = \frac{ \det(\boldsymbol \Psi/2)^{k/2} }{\Gamma_d(k/2) } \det(\boldsymbol X)^{-(k+d+1)/2} \exp\left(-\text{Tr}(\boldsymbol \Psi\boldsymbol X^{-1})/2\right) \] As with the Wishart distribution his pdf is a joint pdf over the \(d\) diagonal elements \(x_{ii}\) and the \(d(d-1)/2\) off-diagonal elements \(x_{ij}\) of the symmetric random matrix \(\boldsymbol X\).
The inverse Wishart and the Wishart distributions are linked. If \(\boldsymbol X\sim \text{IW}\left(\boldsymbol \Psi, k\right)\) then the inverse of \(\boldsymbol X\) is Wishart distributed with inverted scale parameter: \[ \boldsymbol X^{-1} \sim \text{Wis}\left( \boldsymbol S= \boldsymbol \Psi^{-1} \, , k \right) \] where \(k\) is the shape parameter and \(\boldsymbol S\) the scale parameter of the Wishart distribution.
If \(\boldsymbol \Psi\) is a scalar \(\psi\) (and \(d=1\)) then the multivariate inverse Wishart distribution reduces to the univariate inverse Wishart distribution (Section 4.5).
The mniw package implements the Wishart distribution. The pdf of the Wishart distribution is given by mniw::diwish(). The corresponding random number generator is mniw::riwish().
Mean parametrisation
Instead of \(\boldsymbol \Psi\) and \(k\) we may also equivalently use \(\boldsymbol M= \boldsymbol \Psi/(k-d-1)\) and \(\kappa = k-d-1\) as parameters for the inverse Wishart distribution, so that \[ \boldsymbol X\sim \text{IW}\left(\boldsymbol \Psi= \kappa \boldsymbol M\, , \, k= \kappa+d+1\right) \] with mean (for \(\kappa > 0\)) \[ \text{E}(\boldsymbol X) =\boldsymbol M \] and variances (for \(\kappa >2)\) \[ \text{Var}(x_{ij})= \frac{\kappa \, \mu_{ii} \mu_{jj} +(\kappa+2) \, \mu_{ij}^2 }{(\kappa + 1)(\kappa-2)} \]
For \(\boldsymbol M\) equal to scalar \(\mu\) with \(d=1\) the above reduces to the univariate inverse Wishart distribution in mean parametrisation.
Biased mean parametrisation
Using \(\boldsymbol T= (t_{ij}) = \boldsymbol \Psi/(k-d+1) = \boldsymbol \Psi/\nu\) as biased mean parameter together with \(\nu=k-d+1\) we arrive at the biased mean parametrisation \[ \boldsymbol X\sim \text{IW}\left(\boldsymbol \Psi= \nu \boldsymbol T\, , \, k=\nu+d-1\right) \]
The corresponding mean is (for \(\nu > 2\)) \[ \text{E}(\boldsymbol X) = \frac{\nu}{\nu-2} \boldsymbol T= \boldsymbol M \] and the variances of elements of \(\boldsymbol X\) are (for \(\nu > 4\)) \[ \text{Var}(x_{ij})= \left(\frac{\nu}{\nu-2}\right)^2 \, \frac{ (\nu-2) \, t_{ii} t_{jj} + \nu \, t_{ij}^2 }{(\nu-1)(\nu-4)} \] As \(\boldsymbol T= \boldsymbol M(\nu-2)/\nu\) for large \(\nu\) the parameter \(\boldsymbol T\) will become identical to the true mean \(\boldsymbol M\).
For \(\boldsymbol T\) equal to scalar \(\tau^2\) with \(d=1\) the above reduces to the univariate inverse Wishart distribution in biased mean parametrisation.
Scale transformation
If \(\boldsymbol X\sim \text{IW}(\boldsymbol \Psi, k)\) then the scaled symmetric random matrix \(\boldsymbol A\boldsymbol X\boldsymbol A^T\) is also inverse Wishart distributed with \(\boldsymbol A\boldsymbol X\boldsymbol A^T \sim \text{IW}(\boldsymbol A\boldsymbol \Psi\boldsymbol A^T, k)\) where the matrix \(\boldsymbol A\) has full rank and both \(\boldsymbol A\boldsymbol X\boldsymbol A^T\) and \(\boldsymbol A\boldsymbol \Psi\boldsymbol A^T\) remain positive definite. The matrix \(\boldsymbol A\) may be rectangular, hence the size of \(\boldsymbol A\boldsymbol X\boldsymbol A^T\) and \(\boldsymbol A\boldsymbol \Psi\boldsymbol A^T\) may be smaller compared to \(\boldsymbol X\) and \(\boldsymbol \Psi\).
5.6 Multivariate \(t\)-distribution
The multivariate \(t\)-distribution \(\text{$t_{\nu}$}(\boldsymbol \mu, \boldsymbol T)\) is a multivariate generalisation of the location-scale \(t\)-distribution \(\text{$t_{\nu}$}(\mu, \tau^2)\) (Section 4.6) from one to \(d\) dimensions. It is a generalisation of the multivariate normal distribution \(N(\boldsymbol \mu, \boldsymbol T)\) (Section 5.3) with an additional parameter \(\nu > 0\) (degrees of freedom) controlling the probability mass in the tails.
Special cases include the multivariate standard \(t\)-distribution \(\text{$t_{\nu}$}(\mathbf 0, \boldsymbol I)\), the multivariate normal distribution \(N(\boldsymbol \mu, \boldsymbol T)\) and the multivariate Cauchy distribution \(\text{Cau}(\boldsymbol \mu, \boldsymbol T)\).
Standard parametrisation
If \(\boldsymbol x\in \mathbb{R}^d\) is a multivariate \(t\)-distributed random variable we write \[ \boldsymbol x\sim \text{$t_{\nu}$}(\boldsymbol \mu, \boldsymbol T) \] where the vector \(\boldsymbol \mu\) is the location parameter (a \(d\) dimensional vector) and the dispersion parameter \(\boldsymbol T\) is a symmetric positive definite matrix of dimension \(d \times d\). The dimension \(d\) is implicit in both parameters. The parameter \(\nu > 0\) prescribes the degrees of freedom. For small values of \(\nu\) the distribution is heavy-tailed and as a result only moments of order smaller than \(\nu\) are finite and defined.
The mean is (for \(\nu>1\)) \[ \text{E}(\boldsymbol x) = \boldsymbol \mu \] and the variance (for \(\nu>2\)) \[ \text{Var}(\boldsymbol x) = \frac{\nu}{\nu-2} \boldsymbol T \]
The pdf of \(\text{$t_{\nu}$}(\boldsymbol \mu, \boldsymbol T)\) is \[ p(\boldsymbol x| \boldsymbol \mu, \boldsymbol T, \nu) = \det(\boldsymbol T)^{-1/2} \frac{\Gamma(\frac{\nu+d}{2})} { (\pi\nu)^{d/2} \,\Gamma(\frac{\nu}{2})} \left(1+ \frac{\Delta^2}{\nu} \right)^{-(\nu+d)/2} \] with \(\Delta^2 = (\boldsymbol x-\boldsymbol \mu)^T \boldsymbol T^{-1} (\boldsymbol x-\boldsymbol \mu)\) the squared Mahalanobis distance between \(\boldsymbol x\) and \(\boldsymbol \mu\). Note that this pdf is a joint pdf over the \(d\) elements \(x_1, \ldots, x_d\) of the random vector \(\boldsymbol x\).
For \(d=1\) the random vector \(\boldsymbol x=x\) is a scalar, \(\boldsymbol \mu= \mu\), \(\boldsymbol T= \tau^2\) and thus the multivariate \(t\)-distribution reduces to the location-scale \(t\)-distribution (Section 4.6).
The mnormt package implements the multivariate \(t\)-distribution. The function mnormt::dmt() provides the pdf and mnormt::pmt() returns the distribution function. The function mnormt::rmt() is the corresponding random number generator.
Scale parametrisation
The multivariate \(t\)-distribution, like the multivariate distribution, can also be represented with a matrix scale parameter \(\boldsymbol L\) in place of a matrix dispersion parameter \(\boldsymbol T\).
Let \(\boldsymbol L\) be a matrix scale parameter such that \(\boldsymbol L\boldsymbol L^T = \boldsymbol T\) and \(\boldsymbol W=\boldsymbol L^{-1}\) be the corresponding inverse matrix scale parameter with \(\boldsymbol W^T \boldsymbol W= \boldsymbol T^{-1}\). By construction \(|\det(\boldsymbol W)|=\det(\boldsymbol T)^{-1/2}\) and \(|\det(\boldsymbol L)|=\det(\boldsymbol T)^{1/2}\).
Note that \(\boldsymbol T\) alone does not fully determine \(\boldsymbol L\) and \(\boldsymbol W\) due to rotational freedom, see the discussion in Section 5.3 for details.
Special case: multivariate standard \(t\)-distribution
With \(\boldsymbol \mu=\mathbf 0\) and \(\boldsymbol T=\boldsymbol I\) the multivariate \(t\)-distribution reduces to the multivariate standard \(t\)-distribution \(\text{$t_{\nu}$}(\mathbf 0,\boldsymbol I)\). It is a generalisation of the multivariate standard normal distribution \(N(\mathbf 0,\boldsymbol I)\) to allow for heavy tails.
The distribution has mean \(\text{E}(\boldsymbol x)=\mathbf 0\) (for \(\nu>1\)) and variance \(\text{Var}(\boldsymbol x)=\frac{\nu}{\nu-2}\boldsymbol I\) (for \(\nu>2\)).
The pdf of \(\text{$t_{\nu}$}(\mathbf 0,\boldsymbol I)\) is \[ p(\boldsymbol x| \nu) = \frac{\Gamma(\frac{\nu+d}{2})} { (\pi \nu)^{d/2} \,\Gamma(\frac{\nu}{2})} \left(1+ \frac{ \boldsymbol x^T \boldsymbol x}{\nu} \right)^{-(\nu+d)/2} \] with the squared Mahalanobis distance reducing to \(\Delta^2=\boldsymbol x^T \boldsymbol x\).
For scalar \(x\) (and hence \(d=1\)) the multivariate standard \(t\)-distribution reduces to the Student’s \(t\)-distribution \(\text{$t_{\nu}$}=\text{$t_{\nu}$}(0,1)\).
Unlike the multivariate standard normal distribution, the density of the multivariate standard \(t\)-distribution cannot be written as product of corresponding univariate standard densities.
Special case: multivariate normal distribution
For \(\nu \rightarrow \infty\) the multivariate \(t\)-distribution \(\text{$t_{\nu}$}(\boldsymbol \mu, \boldsymbol T)\) reduces to the multivariate normal distribution \(N(\boldsymbol \mu, \boldsymbol T)\) (Section 5.3). Correspondingly, for \(\nu \rightarrow \infty\) the multivariate standard \(t\)-distribution \(\text{$t_{\nu}$}(\mathbf 0,\boldsymbol I)\) becomes equal to the multivariate standard normal distribution \(N(\mathbf 0,\boldsymbol I)\).
This can be seen from the corresponding limits of the two factors in the pdf of the multivariate \(t\)-distribution that depend on \(\nu\):
Following Sterling’s approximation for large \(x\) we can approximate \(\log \Gamma(x) \approx (x-1) \log(x-1)\). For large \(\nu\) this implies that \[\frac{\Gamma((\nu+d)/2)} {(\pi\nu)^{d/2} \,\Gamma(\nu/2)} \rightarrow (2\pi)^{-d/2}\]
For small \(x\) we can approximate \(\log(1+x) \approx x\). Thus for large \(\nu \gg d\) (and hence small \(\Delta^2 / \nu\)) this yields \((\nu+d) \log(1+ \Delta^2 / \nu) \rightarrow \Delta^2\) and hence \(\left(1+ \Delta^2 / \nu \right)^{-(\nu+d)/2} \rightarrow e^{-\Delta^2/2}\).
Hence, the pdf of \(\text{$t_{\infty}$}(\boldsymbol \mu, \boldsymbol T)\) is the multivariate normal pdf \[ p(\boldsymbol x| \boldsymbol \mu, \boldsymbol T, \nu=\infty) = \det(\boldsymbol T)^{-1/2} (2\pi)^{-d/2} e^{-\Delta^2/2} \]
Special case: multivariate Cauchy distribution
For \(\nu=1\) the multivariate \(t\)-distribution becomes the multivariate Cauchy distribution \(\text{Cau}(\boldsymbol \mu, \boldsymbol T)=\text{$t_{1}$}(\boldsymbol \mu, \boldsymbol T)\).
Its mean, variance and other higher moments are all undefined.
It has pdf \[ p(\boldsymbol x| \boldsymbol \mu, \boldsymbol T) = \det(\boldsymbol T)^{-1/2} \Gamma\left(\frac{d+1}{2}\right) \left( \pi (1+ \Delta^2 ) \right)^{-(d+1)/2} \]
For scalar \(x\) (and hence \(d=1\)) the multivariate Cauchy distribution \(\text{Cau}(\boldsymbol \mu, \boldsymbol T)\) reduces to the univariate Cauchy distribution \(\text{Cau}(\mu, \tau^2)\).
Special case: multivariate standard Cauchy distribution
The multivariate standard Cauchy distribution \(\text{Cau}(\mathbf 0, \boldsymbol I)=\text{$t_{1}$}(\mathbf 0, \boldsymbol I)\) is obtained by setting \(\boldsymbol \mu=\mathbf 0\) and \(\boldsymbol T=\boldsymbol I\) in the multivariate Cauchy distribution or, equivalently, by setting \(\nu=1\) in the multivariate standard \(t\)-distribution.
It has pdf \[ p(\boldsymbol x) = \Gamma\left(\frac{d+1}{2}\right) \left( \pi (1+ \boldsymbol x^T \boldsymbol x) \right)^{-(d+1)/2} \]
For scalar \(x\) (and hence \(d=1\)) the multivariate standard Cauchy distribution \(\text{Cau}(\mathbf 0, \boldsymbol I)\) reduces to the standard univariate Cauchy distribution \(\text{Cau}(0, 1)\).
Location-scale transformation
Let \(\boldsymbol L\) be a scale matrix for \(\boldsymbol T\) and \(\boldsymbol W\) the corresponding inverse scale matrix.
If \(\boldsymbol x\sim \text{$t_{\nu}$}(\boldsymbol \mu, \boldsymbol T)\) then \(\boldsymbol y= \boldsymbol W(\boldsymbol x-\boldsymbol \mu) \sim \text{$t_{\nu}$}(\mathbf 0, \boldsymbol I)\). This location-scale transformation reduces a multivariate \(t\)-distributed random variable to a standard multivariate \(t\)-distributed random variable.
Conversely, if \(\boldsymbol y\sim \text{$t_{\nu}$}(\mathbf 0, \boldsymbol I)\) then \(\boldsymbol x= \boldsymbol \mu+ \boldsymbol L\boldsymbol y\sim \text{$t_{\nu}$}(\boldsymbol \mu, \boldsymbol T)\). This location-scale transformation generates the multivariate \(t\)-distribution from the multivariate standard \(t\)-distribution.
Note that for \(\nu > 2\) under the location-scale transformation \(\boldsymbol x= \boldsymbol \mu+ \boldsymbol L\boldsymbol y\) with \(\text{Var}(\boldsymbol y)=\nu/(\nu-2) \boldsymbol I\) we get \(\text{Cov}(\boldsymbol x, \boldsymbol y) = \nu/(\nu-2)\boldsymbol L\). This provides a means to choose between different factorisations of \(\boldsymbol T\) and \(\boldsymbol T^{-1}\). For example, if positive correlation between corresponding elements in \(\boldsymbol x\) and \(\boldsymbol y\) is desired then the diagonal elements in \(\boldsymbol L\) must be positive.
For the special case of the multivariate Cauchy distribution (corresponding to \(\nu=1\)) similar relations hold between it and the multivariate standard Cauchy distribution. If \(\boldsymbol x\sim \text{Cau}(\boldsymbol \mu, \boldsymbol T)\) then \(\boldsymbol y= \boldsymbol W(\boldsymbol x-\boldsymbol \mu) \sim \text{Cau}(\mathbf 0, \boldsymbol I)\). Conversely, if \(\boldsymbol y\sim \text{Cau}(\mathbf 0, \boldsymbol I)\) then \(\boldsymbol x= \boldsymbol \mu+ \boldsymbol L\boldsymbol y\sim \text{Cau}(\boldsymbol \mu, \boldsymbol T)\).
Convolution property
The multivariate \(t\)-distribution is not generally closed under convolution, with the exception of two special cases, the multivariate normal distribution (\(\nu=\infty\)), see Section 5.3, and the multivariate Cauchy distribution (\(\nu=1\)) with the additional restriction that the dispersion parameters are proportional.
For the Cauchy distribution with \(\boldsymbol T_i= a_i^2 \boldsymbol T\), where \(a_i>0\) are positive scalars, \[ \sum_{i=1}^n \text{Cau}(\boldsymbol \mu_i, a_i^2 \boldsymbol T) \sim \text{Cau}\left( \sum_{i=1}^n \boldsymbol \mu_i, \left(\sum_{i=1}^n a_i\right)^2 \boldsymbol T\right) \]
Multivariate \(t\)-distribution as compound distribution
The multivariate \(t\)-distribution can be obtained as mixture of multivariate normal distributions with identical mean and varying covariance matrix. Specifically, let \(z\) be a univariate inverse Wishart random variable \[ z \sim \text{IW}(\psi=\nu, k=\nu) = \text{IG}\left(\alpha=\frac{\nu}{2}, \beta=\frac{\nu}{2}\right) \] and let \(\boldsymbol x| z\) be multivariate normal \[ \boldsymbol x| z \sim N(\boldsymbol \mu,\boldsymbol \Sigma= z \boldsymbol T) \] The resulting marginal (scale mixture) distribution for \(\boldsymbol x\) is the multivariate \(t\)-distribution \[ \boldsymbol x\sim \text{$t_{\nu}$}\left(\boldsymbol \mu, \boldsymbol T\right) \]
An alternative way to arrive at \(\text{$t_{\nu}$}\left(\boldsymbol \mu, \boldsymbol T\right)\) is to include \(\boldsymbol T\) as parameter in the inverse Wishart distribution \[ \boldsymbol Z\sim \text{IW}(\boldsymbol \Psi=\nu \boldsymbol T, k=\nu+d-1) \] and let \[ \boldsymbol x| \boldsymbol Z\sim N(\boldsymbol \mu,\boldsymbol \Sigma= \boldsymbol Z) \] Note that \(\boldsymbol T\) is now the biased mean parameter of the multivariate inverse Wishart distribution. This characterisation is useful in Bayesian analysis.